CHAPTER 19
REACTOR PHYSICS FOR LIQUID METAL REACTOR DESIGN94
The flexibility of liquid metal fuel systems is such that they range over several different reactor categories. Liquid metal reactors may be designed as fast, intermediate, or thermal systems, with either circulating or static fuel systems. The reactor core components consist of a fuel carrier such as molten bismuth or lead, and a moderator such as graphite or beryllium, if the neutrons within the reactor core are to be thermalized. If the fuel is stationary, a second fluid is required as the reactor coolant.
In the simplest system, a high-temperature liquid-metal solution or slurry would be pumped through an externally moderated reactor core. For such a reactor, the neutron physics problems would be similar to those of aqueous homogeneous systems. The chief difference would lie in the neutron spectrum, which would be higher because of weaker moderation and higher operating temperatures.
The liquid-metal system that has received the greatest emphasis to date is of the heterogeneous, circulating fuel type. This reactor, known as the Liquid Metal Fuel Reactor (LMFR), has as its fuel a dilute solution of enriched uranium in liquid bismuth, and graphite is used as both moderator and reflector. With U233 as the fuel and Th232 as the fertile material, the reactor can be designed as a thermal breeder. Consideration is restricted here to this reactor type but, wherever possible, information of a general nature is included.
19-1. LMFR Parameters
19-1.1 Cross sections.
Most of the cross sections required for neutron physics studies of the LMFR can be obtained from BNL-325. The following exceptions should be noted. The 2200 m/sec value of the absorption cross section of graphite is given as 3.2 ± 0.2 mb. The best experimental value however is 3.6 mb after correcting for the presence of such impurities as B, N2, etc. Graphite of density 1.65 to 1.70 g/cm3 is obtainable with an absorption cross section of about 4 mb, including impurities. Graphite of density 1.8 g/cm3 or higher is becoming available, but the purity of this high-density graphite has not been well established.
The 2200 m/sec value of the absorption cross section of Bi209 is 32 ± 2 mb. Two isomeric states of Bi210 are formed, one of which decays by β-emission with a half-life of 5 days into Po210.
Table 19-1
Parameters of Bi209 Resonances
Eo(ev) |
σ0Г, barn-ev |
Г, ev |
| 810 | 9400 | 5.8 ± 0.3 |
| 2370 | 7660 | 17 ± 1.5 |
Bismuth has prominent resonances at 810 ev and 2370 ev, largely due to scattering. Breit-Wigner parameters obtained by Bollinger et al. at Argonne National Laboratory are listed in Table 19-1. To determine neutron capture within these resonances, it is necessary to estimate the value of the level width, Гγ. One method is to use the value of 0.5 b obtained by Langsdorf (ANL--4342) for the resonance integral, which implies that Гγ is about 150 mv. An analysis of Bollinger's data indicates that a more likely value is about 50 mv.
High-energy cross sections of bismuth and lead are of secondary interest in well-moderated liquid-metal reactors, but would become of prime interest in fast- or intermediate-energy reactors. On the basis of the known levels and spin assignments for bismuth and lead, Oleksa of Brookhaven National Laboratory has calculated cross sections that are in good agreement with experimental data. The (n, p) and (n, a) cross sections are negligible. The threshold for the (n, 2n) cross section in bismuth is high, 7.5 Mev. At 1.0 and 4.3 Mev the transport cross sections of bismuth are calculated as 4.3 b and 4.2 b, respectively. The capture cross section at 1 Mev is 3.4 mb.
Inelastic scattering in bismuth is important in considering fission-energy neutrons. The results of Oleksa's studies are presented in Table 19--2. The lowest levels in Bi209 occur at 0.9, 1.6, 3.35 Mev, respectively. At energies up to 2.6 Mev, Oleksa finds that the cross sections for scattering into the individual levels are in good agreement with calculations based on the Hauser-Feshbach model.
In a U-fueled liquid-metal system, the cross sections of the higher isotopes or uranium are of considerable importance in determining equilibrium concentrations of these isotopes and the time required to approach their equilibrium. These equilibrium conditions require study because of solubility limitations in a liquid-metal fuel reactor. The chain starts with either U235 or U233, depending on whether a converter or breeder reactor is under consideration, and ends with U237 because of its short half-life. In addition, some U238 may be present in the fuel. Thermal cross sections are given in BNL-325.
Other absorption cross sections of importance to high-power, high-fuel burnup reactors are those of the long-lived fission products and, in a U233 breeder, that of Pa233 Despite a number of comprehensive studies of these effects, accurate values may not be known until such reactors have been in operation for some time. Fuel-processing studies for the LMFR, however, indicate that the poisoning effect can economically be maintained at a few percent.
Although the LMFR is a heterogeneous reactor, the fuel and moderator arrangements that have been proposed yield a core which is nearly homogeneous from the neutron physics viewpoint. The preferred core is an impermeable graphite structure perforated with holes of about 2 in. diameter for passage of the liquid-metal fuel. The moderator volume is about equal to that of the liquid metal, bismuth, which contains about 0.1 w/o enriched uranium. Actually, the size of the fuel channels could be considerably increased without seriously increasing the flux disadvantage factor and, hence, the critical mass of the reactor core.
19-1.2 Neutron age and diffusion length.
The following formulas, appropriate for mixtures, have been used to obtain the diffusion area, L2, and neutron age, τ, of graphite-bismuth LMFR cores:
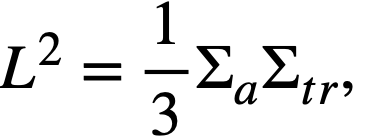 (19-1)
(19-1)
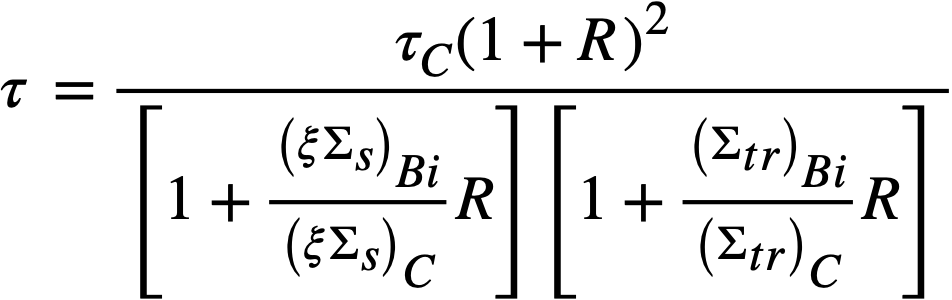 (19-2)
(19-2)
where ξ is the logarithmic energy decrement,
Σs is the macroscopic scattering cross section,
Σa is the macroscopic absorption cross section,
Σtr is the macroscopic transport cross section,
the subscripts Bi and C indicate the macroscopic cross section for the respective materials, and R is the bismuth-to-graphite volume ratio.
19-1.3 Reactivity effects.
A problem unique to circulating fuel reactors is the loss of delayed neutrons in the external circuit. Since the time spent by the delayed-neutron emitters outside the reactor core is generally greater than that spent within the core, a considerable fraction of the delayed neutrons may be wasted. In addition, since most of the delayed-neutron emitters are produced as gases, they may be carried off during degassing operations. For U233, the delayed neutron fraction in thermal fission is only 0.24%. Thus prompt critical may, in some cases, be as little as 0.1% excess reactivity.
Table 19-2
Inelastic Scattering Cross Section of Bi
E,Mev |
σinBi, barns |
| 0.9 | 0 |
| 1.0 | 0.1 |
| 1.5 | 0.4 |
| 2.0 | 0.7 |
| 3.0 | 1.4 |
| 4.0 | 2.0 |
| 5.0 | 2.4 |
| 6.0 | 2.6 |
| 7.0 | 2.6 |
| 8.0 | 2.5 |
| 10.0 | 1.5 |
Coupled with this problem is the fact that the prompt temperature coefficient (due to liquid metal expansion) in the LMFR system under consideration is of the order of -5 x 10-5/°C. Thus, ignoring temperature overshoots, which are discussed later, the magnitude of rapid reactivity changes must be limited to avoid large metal temperature changes. The total temperature coefficient of the LMFR runs about -1.5 x 10-4/°C, the delayed coefficient resulting primarily from increased neutron leakage due to the heating of the graphite structure. While the slow response of the graphite to power changes thus limits the size of the prompt temperature coefficient, it aids in stabilizing the system against small oscillations at high power output.
19-1.4 Breeding.
The LMFR can be operated as a breeder on the U233–Th232 cycle. The possible breeding gain is not large, since the value of η for U233 is about 2.3. The theoretical gain is at most 0.3, but a value of 0.10 is about the maximum possible in a practical system. In fact, optimization based on economic considerations would probably reduce the gain to zero in any power breeder built in the near future. The gain is reduced by competitive neutron capture in the core and blanket, and by neutron leakage from the blanket and from the ends of the reactor core. A problem not yet solved is that of a leakproof, weakly absorbing container that will separate the core and blanket. It is hoped that beryllium or an impermeable graphite will provide such a container for the LMFR Croloy steel or tantalum containers about 1/4-in thick appear satisfactory from the mechanical and metallurgical standpoint but effectively wipe out the potential breeding gain because of their absorption cross section.
A number of studies of the so-called immoderation principle have been carried out in an attempt to reduce the neutron losses to the container. By removing the bulk of the moderator from a small region on both sides of the container wall the thermal neutron losses can be greatly reduced. Several feasible mechanical designs embodying this principle have been worked out by the Babcock & Wilcox Company.
19-2. LMFR Statics
19-2.1 Core.
The standard LMFR is predominantly thermal, nearly homogeneous, and moderated by graphite. Thus age-diffusion theory is applicable, and therefore the following formula can be used for a critical system:
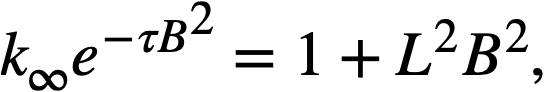 (19-3)
(19-3)
where B2 is the buckling of the system, and
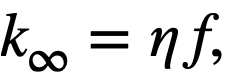 (19-4)
(19-4)
where η is the number of fast neutrons produced per thermal neutron captured in the fuel, and f is the thermal utilization factor. The product of the fast fission effect, ϵ, and resonance escape probability, p, is assumed equal to unity.
In view of the uncertainty in the value of Гγ for bismuth, the validity of neglecting resonance capture is still uncertain, and Monte Carlo studies are planned at BNL to obtain lower limits for p as a function of channel size and lattice pitch. For small channels, the homogeneous formula for f is adequate, since consideration of self-shielding of the fuel reduces f in a typical core by about 2%.
Studies have yielded for buckling the typical values given in Table 19-3 [1] for both U233 and U235 as the fuel in a graphite moderator at an average core temperature of 475°C.
19-2.2 Reflector.
In order to apply the above results to reflected reactors, it is necessary to determine the-reflector savings, which can be obtained from conventional two-group theory. This method could also be used to estimate the critical size of the reactor but, for small cores, two-group theory underestimates the size of graphite-moderated reactors.
Two-group results obtained for typical reflectors are given in Table 19-4 [1] for a cylindrical reactor system surrounded by a large reflector.
Table 19-3
Buckling Of Graphite-Moderated LMFR Cores
VBi/VC |
NU/NBi = 0.6 x 10-3 | NU/NBi = 1 x 10-3 | NU/NBi = 1.5 x 10-3 |
U233 Fuel |
|||
| 0.25 | 6.64 X 10-4cm-2 | 9.51 X 10-4cm-2 | 11.85 X 10-4cm-2 |
| 0.50 | 8.20 | 10.70 | 12.50 |
| 1.00 | 8.09 | 9.82 | 10.95 |
| 1.50 | 7.33 | 8.60 | 9.43 |
| 2.00 | 6.59 | 7.60 | 8.22 |
U235.Fuel |
|||
| 0.25 | 6.05 | 8.65 | 10.72 |
| 0.50 | 7.43 | 9.63 | 11.19 |
| 1.00 | 7.25 | 8.74 | 9.71 |
| 1.50 | 6.53 | 7.64 | 8.30 |
| 2.00 | 5.68 | 6.72 | 7.23 |
Table 19-4
Reflector Savings of U235-Bi Cores Moderated by Graphite
| Reflector |
Core |
||||
|
1 | 2 | 1 | 2 | |
VBi/VC =
|
|||||
| Reflector | NU/NBi= | 0.6 x 10-3 | 0.6 x 10-3 | 1.5 x 10-3 | 1 x 10-3 |
| Graphite |
|
1. 71 ft | 2.10 ft | 1.66 ft | 2.10 ft |
| 9O%C-1O% Void |
|
1.62 | 2.00 | 1.63 | 2.01 |
| VC—VBi—VTh: |
|
|
|
|
|
| 85- 5- 0 |
|
1.69 | 2.04 | 1.65 | 2.04 |
| 85-15- 0 |
|
1.66 | 1.97 | 1.59 | 2.01 |
| 85-10- 5 |
|
0.70 | 0.82 | 0.78 | 0.87 |
| 70-20-10 |
|
0.58 | 0.68 | 0.65 | 0.73 |
19-2.3 Critical mass.
The results of age-diffusion theory are in good agreement with multigroup calculations for predominantly thermal LMFR reactors. At higher fuel concentrations, however, the age theory overestimates the critical mass, as shown in Table 19-5 [1]. The differences in critical mass estimates are large only for weakly moderated reactors.
Table 19-5
Critical Mass and Diameter of U235-Fueled LMFR
Spheres With a 90-cm Graphite Reflector
| Nu/NBi | VBi—U/Vc | Age-Diffusion | Multigroup | ||
|
|
Diameter, ft | Mass, kg | Diameter, ft | Mass, kg |
| Graphite-moderated | |||||
| 1 x 10-3 | 0.25 | 4.38 | 2.73 | 4.52 | 3.02 |
|
1.0 | 3.88 | 4.77 | 3.81 | 4.53 |
|
2.0 | 4.15 | 7.79 | 4.04 | 7.15 |
| 1 x 10-2 | 0.25 | 2.57 | 5.50 | 2.28 | 3.89 |
|
1.0 | 2.79 | 17.69 | 2.24 | 9.20 |
| Beryllium-moderated | |||||
| 1 x 10-3 | 0.25 | 3.86 | 1.87 | 3.88 | 1.92 |
|
1.0 | 3.08 | 2.37 | 2.94 | 2.07 |
|
2.0 | 3.29 | 3.86 | 3.04 | 3.05 |
| 1 x 10-2 | 0.25 | 1.90 | 2.22 | 1.66 | 1.49 |
|
1.0 | 2.11 | 7.70 | 1.73 | 4.19 |
|
2.0 | 2.43 | 15.55 | 1.94 | 7.87 |
19-2.4 Breeding.
The conversion ratio obtainable in liquid metal systems depends on a number of variables, such as the fuel and fertile material concentrations, the fission-product processing methods, losses to the core container, etc. In a feasibility study of the LMFR conducted by the Babcock & Wilcox Company, currently practical reactor designs were reported (BAW-2) with conversion ratios ranging from 0.8 to 0.9, depending on whether an oxide slagging or fused salt method was used for nonvolatile fission-product processing. The U/Bi atomic ratio was low (0.8 x 10-3) and a 2¼% Cr-1 % Mo steel core container was used, both choices tending to reduce the possible breeding ratio. The estimates of the neutron balance are given in Table 19-6 [6].
Table 19-6
Neutron Balance of Th232, U233 Breeder
| Production per U233 absorption | Scheme A Oxide slagging 2.31 |
Scheme B Fused-salt process 2.31 |
| Losses: Absorption in |
|
|
| U233 | 1.00 | 1.00 |
| Bi | 0.13 | 0.13 |
| C | 0.05 | 0.05 |
| Fission products | 0.12 | 0.03 |
| Higher isotopes | 0.02 | 0.02 |
| Croloy structure | 0.12 | 0.12 |
| Th | 0.80 | 0.89 |
| Pa | 0.02 | 0.02 |
| Leakage | 0.05 | 0.05 |
19-2.5 Control.
Because of its prompt temperature coefficient, the LMFR is expected to be stable. Nevertheless, it represents a completely new and untested system. There are a number of ways in which the reactivity of the system can change, for example, with changes in inlet temperature, concentration, or velocity of the fuel, and changes in xenon concentration, delayed neutron emitter concentration, and blanket composition. Most of these changes are expected to be gradual, but they can be sufficiently large to require the use of control rods. Inherent stability has not been demonstrated in operating reactors except over a limited range in reactivity and power output. In a reactor with a high-velocity coolant there may occur sudden changes of reactivity which are too fast for conventional control. Thus both inherent stability against sudden reactivity changes and control rods for large but gradual reactivity changes are needed until considerable experience has been gained in operation of the reactor.
Studies have been carried out at BNL on control requirements for an LMFR experiment. The control requirements depend not only on the choice of operating temperatures, the possible xenon and fission-product poisoning, etc., but also on conceivable emergency situations such as errors in fuel concentration control. In a reactor with a full breeding blanket, the control requirements may have to include the effect of complete loss of the breeder fluid.
For a 5-mw experiment, control of 1.5% reactivity appears to be ample and can be obtained with four 2¼% Cr-1% Mo steel rods of about 2-in. diameter. Blacker rods containing boron could, of course, be used to increase reactivity control. A study of various arrangements of identical rods in a ring around a central rod indicates that the optimum position of the ring occurs at about 1/4 of the distance from the reactor center to the (extrapolated) radius of the reactor core.
It would be highly desirable to use sheaths for control rods in order to eliminate the problem of rod insertion through a heavy liquid metal. Steel sheaths are not satisfactory, since they reduce the breeding ratio in a liquid-metal power breeder and reduce the over-all thermal flux in an experimental reactor. The solution to the problem may lie in the development of structurally sound beryllium sheaths.
19-2.6 Shielding.
Shielding of an LMFR is complicated by the necessity of shielding an external circuit in which the delayed neutron emitters and fission products decay.
Calculations by K. Spinney at BNL indicate that even for a 5-Mw experimental reactor, about 5.5 ft of concrete are required as a neutron shield around the reactor cell. Gamma shielding of the cell requires about 8.5 ft of ordinary concrete or 4.5 ft of BNL concrete (70% Fe). For this reason, it has been proposed that heavy concrete be used as the shield for the 5-Mw reactor. For the rest of the circuit, including the degasser, pumps, heat exchanger, etc., the advantage of using BNL concrete is less evident.
19-3. LMFR Kinetics
A number of fundamental studies of the kinetics of circulating fuel reactors have been carried out at ORNL and by Babcock & Wilcox Company. A review of the subject has been given by Welton [2]. At low power, the equations governing the system are linear and complicated chiefly by the feedback of delayed neutrons. General results for the in-hour relation have been obtained by Fleck [3] for U233_ and U235_ fueled reactors. At high power, the kinetics are much more complicated and there is a real question whether the response of a complex reactor can be accurately predicted in advance of its operation. Bethe [6] has strongly recommended the use of oscillator experiments to determine reactor transfer functions. Despite such experiments, however, the mechanism responsible for the resonances observed in EBR-1 has, to date, not been satisfactorily explained.
There are two methods of treating the kinetics of a reactor. In the open-loop method, the inlet temperature is taken as constant. The justification for this procedure is that this condition generally prevails during rapid transients, the feedback of information through the external system being slow by comparison. The method, however, suffers from the defect that it cannot reveal instabilities associated with the entire circuit. In the closed-loop method, the external system, or a reasonable facsimile, is coupled to the reactor system. The representation of the reactor, however, is generally oversimplified because of the complexity of the over-all system.
Although the set of kinetic equations that include temperature effects are nonlinear, the linearized equations are satisfactory for the investigation of stability and the qualitative transient behavior. A large subset of equations is required to properly treat the effect of the delayed neutron emitters. Again, however, lumping the delayed neutrons into a single group, or neglecting them altogether, always appears to lead to qualitatively, if not quantitatively, correct results.
A study of the temperature-dependent open-loop kinetics of the LMFR has been carried out by Fleck [4]. The effect of delayed neutrons and the delayed moderator temperature coefficient were neglected. Under these conditions, Fleck found that the reactor responded rapidly and with little overshoot in temperature when subjected to the largest permissible reactivity excursions.
Using a method developed at the Oak Ridge National Laboratory (ORNL-CFl-56-4-183) for homogeneous systems, the Babcock & Wilcox Company has studied the stability of the LMFR against small oscillations. The results show that the LMFR models under study are stable up to power densities 100 to 1000 times greater than the nominal design level.
Fleck has also examined the transient pressures in LMFR cores by treating the bismuth as a frictionless, compressible fluid. He found that the maximum pressures developed during conceivable transients were quite small. The assumption sometimes made, that the fluid external to the core can be represented as an incompressible slug, was found to overestimate the transient pressures.
In general, heterogeneous reactors possessing both a small prompt (positive or negative) fuel temperature coefficient and a large delayed negative moderator temperature coefficient can be expected to exhibit oscillatory instability at sufficiently high power. However, elementary models indicate that power levels high enough to cause such instability are not achievable in present reactors. Further study of the complex heat- transfer transients in reactor systems is still required before reactor stability can be assured.
References
1. J. Chernick, Small Liquid Metal Fueled Reactor Systems, Nuclear Sci. and Eng. 1(2), 135 (1956).
2. T. A. Welton, Kinetics of Stationary Reactor Systems, in Proceedings of the International Conference on the Peaceful Uses of Atomic Energy, Vol. 5. New York: United Nations, 1956. (P/610, p. 377)
3. J. A. Fleck, Jr., Theory of Low Power Kinetics of Circulating Fuel Reactors with Several Groups of Delayed Neutrons, USAEC Report BNL-334, Brookhaven National Laboratory, April 1955.
4. J. A. Fleck, Jr., The Temperature Dependent Kinetics of Circulating Fuel Reactors, USAEC Report BNL-357, Brookhaven National Laboratory, .July 1955.
5. G. T. Trammell, Oak Ridge National Laboratory, 1955. ORNL-1893,1955.
6. BABCOCK & WILCOX Co., Liquid Metal Fuel Reactor; Technical Feasibility Report, USAEC Report BAW-2(Del.), June 30, 1955.